Diffrence between likelihood and others

이는 본인의 해석이 많이 들어가 있으니 주의하길 바란다.

Likelihood와 Conditional Probability의 차이

x를 어떤 데이터라고 하고 θ를 통계적인 모델링을 하기 위한 어떤 파라미터라고 할 때, Likelihood 다음과 같은 식으로 표현된다.

Likelihood = L(θ; x) = P(x | θ)

위의 식처럼 θ에 대한 Likelihood는 θ를 주어졌을 때 x가 나타날 Conditional probability를 통해 구해질 수 있으며 이러한 관계가 등호로 표현되지만 이 둘은 서로 다른 개념이다.

이를 개략적으로 설명하면, x에 대한 conditional probability는 Domain이 x인 반면 θ에 대한 Likelihood는 Domain이 θ이기 때문이다.

이를 설명하기 위한 추상적인 수준에서의 예를 들어보겠다.
x와 θ는 다음과 같은 집합을 표현하기 위한 symbol이라고 하자.

θ = {θ1, θ2}
x = {x1, x2, x3}

Likelihood, L(θ; x)는 특정한 x를 가정했을 때, θ의 값이 관측되면 그 θ를 특정한 값으로 사상시키는 함수이므로 다음과 같이 Likelihood 함수의 분포는 L(θ1; x1) 와 L(θ2; x1) 으로 나타낼 수 있다.

반면 는 특정한 θ를 가정하고 x를 Domain으로 바라보기 때문에 다음과 같이 Conditional Probability 함수값의 분포를 나타낼 수 있다. ex) , ,

정리하자면 어떤 symbol을 Domain으로 놓느냐에 따라서 Likelihood 인지 혹은 Conditional Probability인지가 결정된다.

Understanding with Python(2d)

이를 파이썬 코드와 함께 이해해보자.
이 예제에서는 동전던지기 실험을 수행하며, n번 동전이 던져졌을 때 앞면이 몇번이나 나올지에 대한 확률을 모델링하며 x는 앞면이 나올 횟수, θ는 동전이 앞면이 나올 확률을 의미한다.
만약 θ의 값이 0.5라면, 그 동전은 공평한 동전이며 0.5보다 크다면 앞면이 나올 확률이 뒷면이 나올 확률보다 크므로 불공평한 동전이 된다.

아래의 소스코드는 x에 대한 conditional probability의 분포를 그린다.

from scipy.stats import binom
import matplotlib.pyplot as plt
%matplotlib inline

import numpy as np
import itertools

n = 10 # 시행의 횟수
X = np.arange(0, n + 1) # 앞면이 나오는 횟수

dθ = 0.05
all_θ = np.round(np.arange(0, 1 + dθ, dθ), 4)

first_θ = 0.5

def p_θ(θ):
    # Prior
    return 1/ len(all_θ)

def p_x_givenθ(x, n, θ):
    # P(x|θ)
    return np.round(binom.pmf(x, n, θ), 3)

def p_θ_givenX(θ, n, x, all_θ, prior):
    # P(θ|x)
    likelihood = p_x_givenθ(x, n, θ)
    prob_θ = prior(θ)
    p_x = sum([p_x_givenθ(x=x, n=n, θ=temp_θ) * prior(temp_θ) for temp_θ in all_θ])
    
    return np.round((likelihood * prob_θ) / p_x, 3)

fig, ax = plt.subplots(1, 1)

v_p_x_givenθ = p_x_givenθ(X, n=n, θ=first_θ)

ax.plot(X, v_p_x_givenθ, 'bo', ms=8)
ax.vlines(X, ymin=0, ymax=v_p_x_givenθ, colors='b', lw=5, alpha=0.5)

plt.xticks(X, X)

plt.ylabel("$p(x|θ= {first_θ:.2f})$".format(first_θ = first_θ))
plt.xlabel("x")

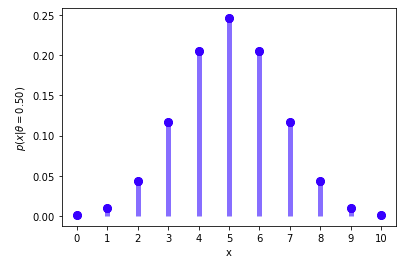
아래의 소스 코드는 θ에 대한 Likelihood를 구한다.

fig, ax = plt.subplots(1, 1)

target_x = 7

v_p_x_givenθ = p_x_givenθ(target_x, n=n, θ=all_θ)

ax.plot(all_θ, v_p_x_givenθ, 'ro', ms=8, label='binom pmf')
ax.vlines(all_θ, ymin=0, ymax=v_p_x_givenθ, colors='r', lw=5, alpha=0.5)

plt.xticks(all_θ, all_θ, rotation=90)
plt.ylabel("$L(θ; x = {target_x:.1f})$".format(target_x = target_x))
plt.xlabel("θ")

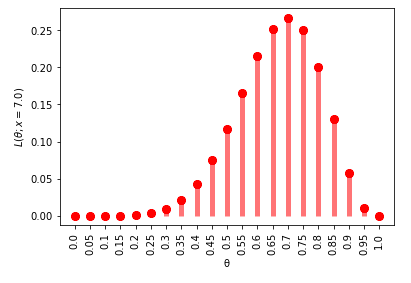
위 두 소스 코드 모두 p_x_givenθ라는 함수를 사용하여 분포를 표현하지만, x를 Domain으로 할지 혹은 θ를 Domain으로 할지에 따라 분포의 형태가 달라졌다.
이것이 Likelihood와 Conditional probability간의 차이이다.

Understanding with Python(3d)

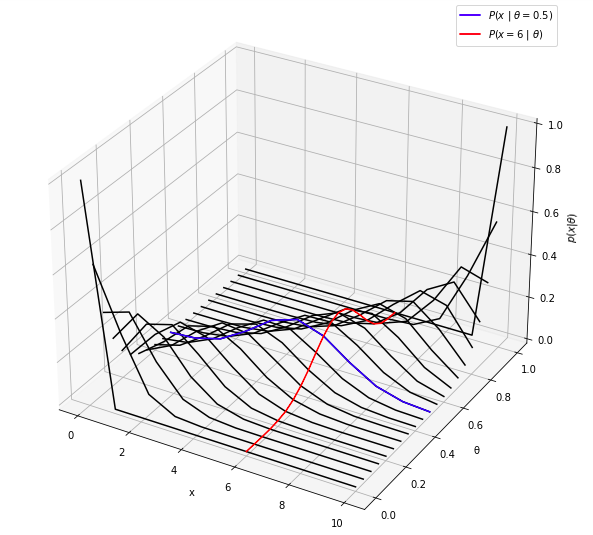
이를 3차원으로 표현해보면 더욱 쉽게 이해할 수 있다.
아래 그래프의 빨간색 선은 θ를 Domain으로 본 것이며 파란색 선은 x를 Domain으로 본 것이다.
따라서 빨간선은 θ에 대한 Likelihood의 분포이고 파란선은 x에 대한 Conditional Probability의 분포이다.

def str_join(strs, deliminator = "_"):
    """
    join string

    :param strs: list of string
    :param deliminator: deliminator

    return: combination string
    """
    strs = list(filter(lambda str: str != "", strs))
    
    if len(strs) == 1:
        return str(strs[0])
    else:
        return strs[0] + deliminator + str_join(strs[1:], deliminator)
    
def get_function_args(function_name, module_name = "__main__"):
    """
    function args
    
    :param module_name: module name(string) ex) sys.modules[__name__]
    :param function_name: function name(string) ex) clean
    
    return: arg names of function(list)
    """
    import inspect
    func = getattr(sys.modules[module_name], function_name)
    return func, inspect.getfullargspec(func)[0]

def multi_mapping(func_name, arg_value_pairs, module_name = "__main__"):
    """
    This function maps multiple input into output
    
    :param function_name: function name(string) ex) "clean"
    :param arg_value_pairs: arguments(list) ex) [[1, 2], [3, 4]]
    :param module_name: module name(string) ex) sys.modules[__name__]
    
    return: outpus of function(list)
    """
    func, arg_names = get_function_args(module_name = module_name, function_name = func_name)
    
    return list(map(lambda arg_value_pair: call_func_dynamically(function_name = func_name, 
                                                          argument_names = arg_names, 
                                                          arg_value_pair = arg_value_pair) ,
             arg_value_pairs))
    
def call_func_dynamically(function_name, argument_names, arg_value_pair, module_name = "__main__"):
    """
    Call function using string expression
    
    :param function_name: function name
    :argument_names: arg names(list) ex) ["a", "b"]
    :arg_value_pair: arg value pair(list) corresponding arg_name ex) [1, 2] <- number or ['1', '2'] <- string
    :param module_name: module name(string) ex) sys.modules[__name__]
    
    return: output of function
    """
    # mapping between arg name and arg value
    arg = list(map(lambda arg_name, arg_value: str_join([arg_name, arg_value], "="), argument_names, arg_value_pair))
    
    # make function call expresion
    func_call = function_name + "(" + str_join(arg, ",") + ")"
    
    # result
    result = eval(func_call, {function_name : getattr(sys.modules[module_name], function_name)})
    
    return result

fig = plt.figure(figsize=(10,10))

ax = fig.add_subplot(projection='3d')

parameter_pairs = np.array(list(itertools.product(X, [n], all_θ)))

Xs = parameter_pairs[:,0]
θs = parameter_pairs[:,2]
probs = np.array(multi_mapping(func_name = "p_x_givenθ", 
                      arg_value_pairs = parameter_pairs, 
                      module_name = __name__))

points = np.array(list(zip(Xs, θs, probs)))

for θ in all_θ:
    target_points = points[np.where(points[:,1] == θ, True, False)]
    ax.plot(target_points[:,0], 
            target_points[:,1], 
            zs=target_points[:,2],
            color="black")

target_θ = 0.5
target_points = points[np.where(points[:,1] == target_θ, True, False)]
plot_givenθ = ax.plot(target_points[:,0], 
        target_points[:,1], 
        zs=target_points[:,2],
        color="blue",
        label="$P(x\ |\ θ = 0.5)$")

target_x = 6
target_points = points[np.where(points[:,0] == target_x, True, False)]
plot_givenX = ax.plot(target_points[:,0], 
            target_points[:,1], 
            zs=target_points[:,2],
            color="red",
            label="$P(x = 6\ |\ θ)$")


ax.set_xlabel("x")
ax.set_ylabel("θ")
ax.set_zlabel("$p(x|θ)$")

ax.legend(handles=plot_givenθ + plot_givenX)

The difference between Posterior and Likelihood

Posterior와 Likelihood는 모두 θ를 Domain으로 바라보기 때문에 혼동이 생길 수 있다.

하지만 이 둘은 값을 구하는 식 자체가 다르기 때문에 서로 다르다.

Posterior의 경우 다음과 같은 식으로 값을 구한다.

반면 Likelihood를 구하는 식은 다음과 같다.

L(θ;x) = P(x|θ)

Posterior와 Likelihood 모두 Domain를 θ로 바라보지만, Posterior function은 확률 공리를 만족시키는 함수인 반면, Likelihood function은 Conditional probability에서 확률 공리를 만족시키는 x를 domain으로 보는 함수가 아닌 θ를 Domain으로 바라보기 때문에 확률 공리를 만족시키지 못한다.

*여기서 말하는 확률 공리는 확률 함수가 모든 가능한 값을 사상시켰을 때의 합이 1이 되는 것을 의미한다.

이 둘을 그래프로 표현하면 다음과 같다.

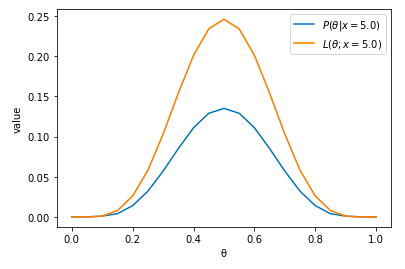
target_x = 5

plt.plot(all_θ, p_θ_givenX(θ=all_θ, n=n, x=target_x, all_θ=all_θ, prior=p_θ))
plt.plot(all_θ, p_x_givenθ(x = target_x, n=n, θ=all_θ))

plt.xlabel("θ")
plt.ylabel("value")

plt.legend(["$P(θ | x)$", "$L(θ; x)$"])
print("Consider all θ")
print("likelihood: ", sum(p_x_givenθ(x = target_x, n=n, θ=all_θ)), "Posterior: ", sum(p_θ_givenX(θ=all_θ, n=n, x=target_x, all_θ=all_θ, prior=p_θ)))

정리

Likelihood와 Conditional Probability의 다른점은 Domain의 대상이다.

Likelihood와 Posterior는 같은 대상을 domain으로 고려하지만, Posterior를 구할때의 function은 확률 공리를 만족시키는 함수인 반면 Likelihood는 그렇지않다.