검정이란?

통계학에서 검정이란 기존의 주장과 대립되는 주장을 제시하였을때 그 주장이 옳은지 검증 하는것을 의미한다.
통계학은 불확실성을 다루는 학문이므로 모든 주장은 불확실성이 존재한다고 생각한다.
예를 들어, “사과는 빨갛다”라는 가설은 항상 옳지 않다. 왜냐하면 초록색 사과가 있을 수 있기 때문인데 이렇듯 “사과는 빨갛다”라는 당연하다 싶은 가설을 다룰 때 조차도 불확실성을 내포하고 있다. 확률 분포는 데이터들을 모아 이러한 불확실성을 표현한다.

앞서 말했듯 통계학은 불확실성을 내포하므로 위의 주장을 다음처럼 나타낼 수 있을 것이다. “사과는 빨갈수도 초록색일수도 있지만 전반적으로는 빨갛다!”

대립 가설

그런데 어느날 아오리 사과라는 사과 품종을 재배하는 어떤 농부는 이렇게 주장하였다. “사과는 초록색이다.” 그러나 앞서 말했듯 통계에 기반한 주장은 불확실성을 동반한다고 하였다. 그래서 위의 명제는 다음과 같이 분포의 형태로 바꿀 수 있다. “사과는 빨갈수도 초록색일수도 있지만 전반적으로 초록색이다!”

검증을 위한 데이터 추출

마을 사람들은 이 대립을 해결하기 위해서 시장에 나가 무작위로 사과를 뽑아서 위의 명제를 검증하기로 하였다. 그랬더니 빨간 사과가 6개 초록 사과가 4개가 나왔다고 해보자. 이 데이터는 사과가 전반적으로 빨갛다라는 주장을 뒷받침하는 근거가 될 수 있을까?

검증

통계학자들은 이와 같은 대립을 다음과 같이 다룬다. “사과는 빨갈수도 초록색일수도 있지만 전반적으로는 빨갛다”라는 주장을 가정하였을 때, 빨간 사과가 7개 초록 사과가 3개가 나올 확률을 계산하고 그 확률을 가지고 가정을 검증한다.

전반적으로 사과가 빨갛다라는 주장을 구체적으로 다뤄보자.
이러한 주장은 사과가 빨간 확률이 0.9 이고 사과가 초록색일 확률이 0.1 이라는 확률 분포로 대응할 수 있다고 해보자.

이제 이 분포를 가정했을때, 추출된 데이터가 어떤 확률을 가질 것인지 계산해보자.
빨간 사과가 6개 뽑혔으니 0.9를 6번 곱하고 초록 사과가 4번 나왔으니 0.1을 4번 곱하자.
그리고 순서를 무시하는 조합을 고려하면 다음과 같은 결과가 된다. 10C6 = 210
그리고 이를 모두 고려하면, 210 * 0.9^6 * 0.1^4 = 0.01이 된다.
즉, 사과는 빨갈수도 초록색일수도 있지만 전반적으로는 빨갛다라는 주장에 대응되는 분포를 가정하였을 때, 0.01의 확률로 마을 사람들이 추출한 데이터가 나온다는 것이다.

귀무가설 기각

통계학자들은 보통 0.05를 기준으로 기존의 주장의 기각 여부를 결정하는데, 이보다 낮으면 기존의 주장을 기각하고 높으면 기존의 주장을 기각하지 않는다.
위 데이터는 0.01이 나왔으므로 사과는 사과는 빨갈수도 초록색일수도 있지만 전반적으로는 빨갛다라는 주장을 기각하게 된다.
이것이 무슨 말이냐면, 사과는 빨갈수도 초록색일수도 있지만 전반적으로는 빨갛다라는 주장은 실제의 현상을 잘 반영하지 못한다는 것이다.

아래의 그래프를 보자.
사과는 전반적으로 빨갛다라는 귀무가설을 가정하였을때의 분포를 표현하였다.
그중 노란색으로 표현된 부분은 마을 사람들이 추출한 데이터가 나올 확률을 나타낸다.

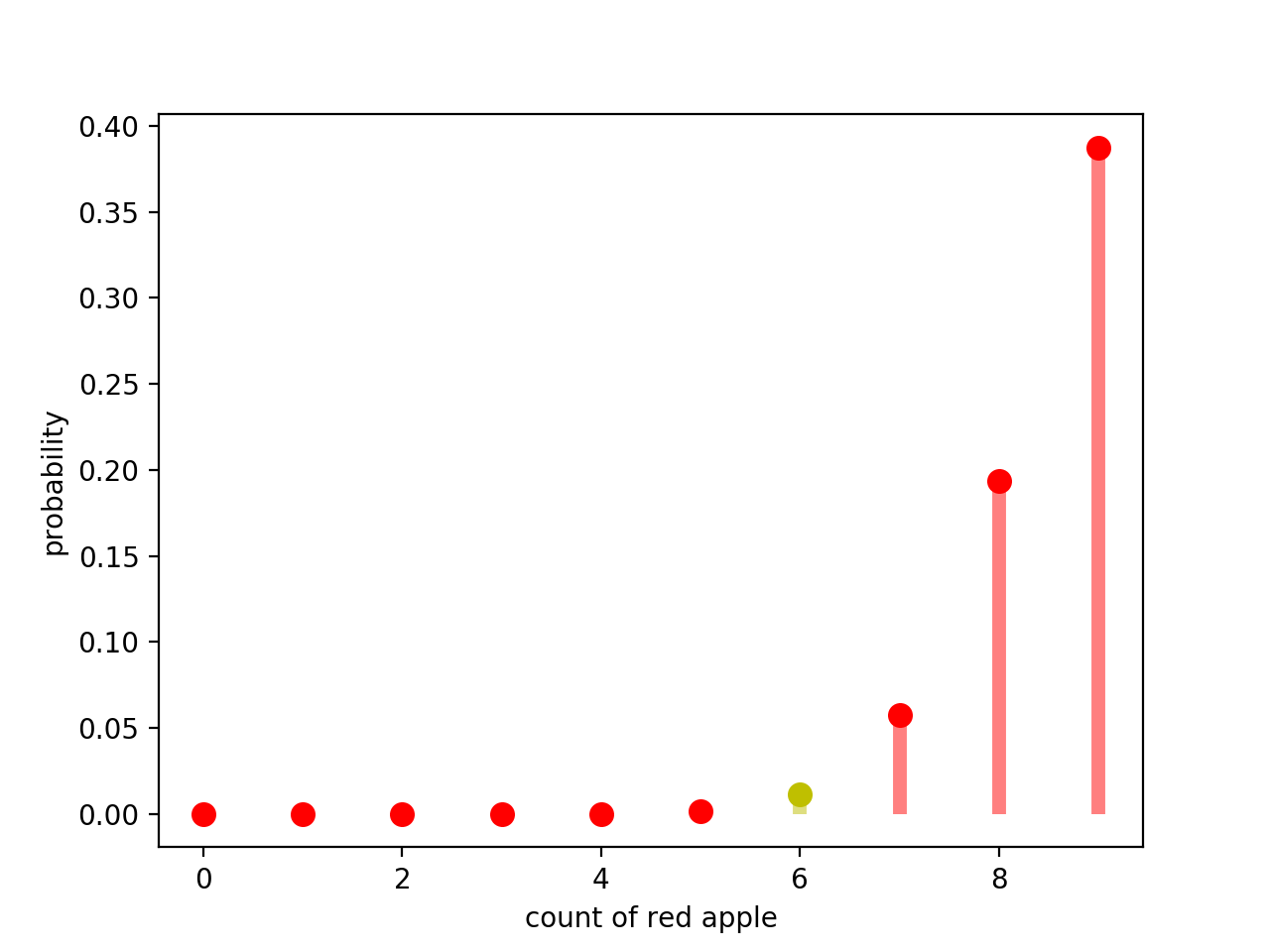
노란색으로 표현된 부분은 한눈에 봐도 아주 낮은 확률을 가지는 것을 알 수 있다.
이 데이터를 근거로 기존에 우리가 가졌던 믿음에 대하여 반박을 할 수 있다.
따라서, 사과는 빨갈수도 초록색일수도 있지만 전반적으로는 빨갛다! 라는 귀무가설은 기각된다.
왜냐하면 빨간색 사과가 나올 확률이 0.9라고 했을 때의 분포가 마을 사람들이 추출한 데이터와 너무 맞지 않기 때문이다.

귀무가설을 기각한다고 해서 대립가설을 채택할 수 있을까?

아래의 그래프를 보자.
이번 그래프는 데이터 추출의 수를 50개로 늘렸을때, 빨간색 사과가 나올 확률이 0.9이고 초록색 사과가 나올때의 확률이 0.1일때를 빨간색 그래프로 표현하였으며(귀무가설) 초록색 사과가 나올 확률이 0.9이고 빨간색 사과가 나올때의 확률이 0.1일때를 초록색 그래프로 표현하였다.(대립가설)

그리고 노란색으로 표현된 부분은 빨간색 사과가 40개, 초록색 사과가 10개 나올 확률을 표현한 것이다. (그래프를 좀 더 예쁘게 표현하기 위하여 샘플의 수를 늘렸다)

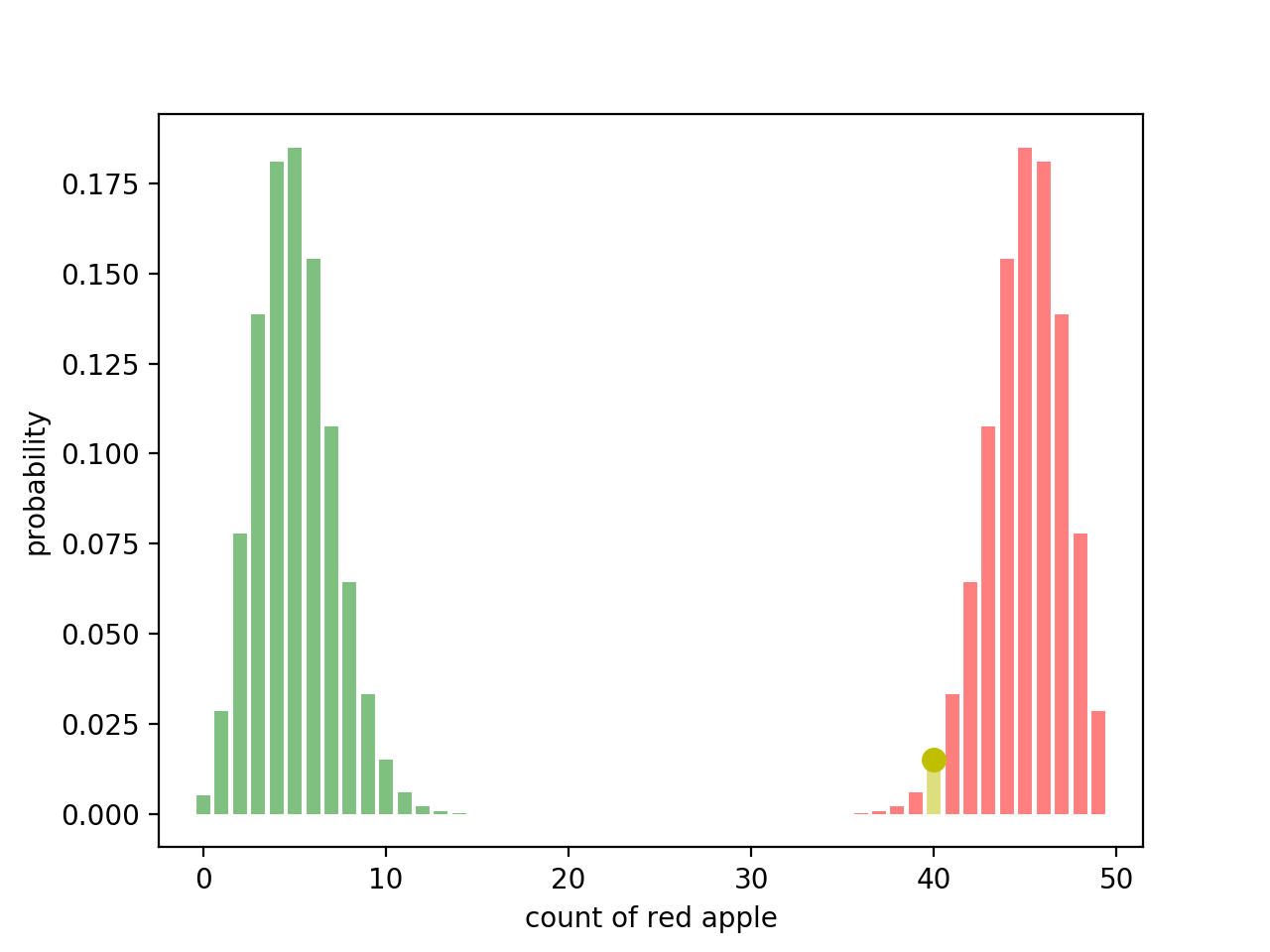
위 그래프를 보면 귀무가설을 가정하였을때의 노란색으로 표현된 부분의 확률이 굉장히 낮은 것을 볼 수 있는 반면 대립가설을 가정하였을때의 초록색으로 표현된 부분의 확률은 더 낮을 것이다.(빨간색 사과가 40개나 나왔으니 당연히 그럴것이다)

이 이야기는 귀무가설을 기각한다고 하여서 바로 대립가설을 채택할 수는 없다는 의미이다.
대립가설을 채택하기 위해서는 더 많은 근거가 필요하다.